Many of the things we play around involve geometric symmetry. There are several types. This post is about an unusual symmetry. But first, a quick recap of some more well-known symmetries…

reflective symmetry

A 2D image has reflective symmetry if you can flip the image over, and the image looks the same, such as this uppercase A in the Futura font:

You can take any image and create reflective symmetry by placing it next to its reflection:

rotational symmetry

An image has rotational symmetry if it is possible to rotate the image less than 360°, and the image looks the same. This letter N is invariant after rotating 180°. We say it has 2-fold rotational symmetry.

You can take any image and create n-fold rotational symmetry by combining n copies of the image, rotating each by a successive multiple of 360°/n. Steamboat Willie has 8-fold rotational symmetry here:

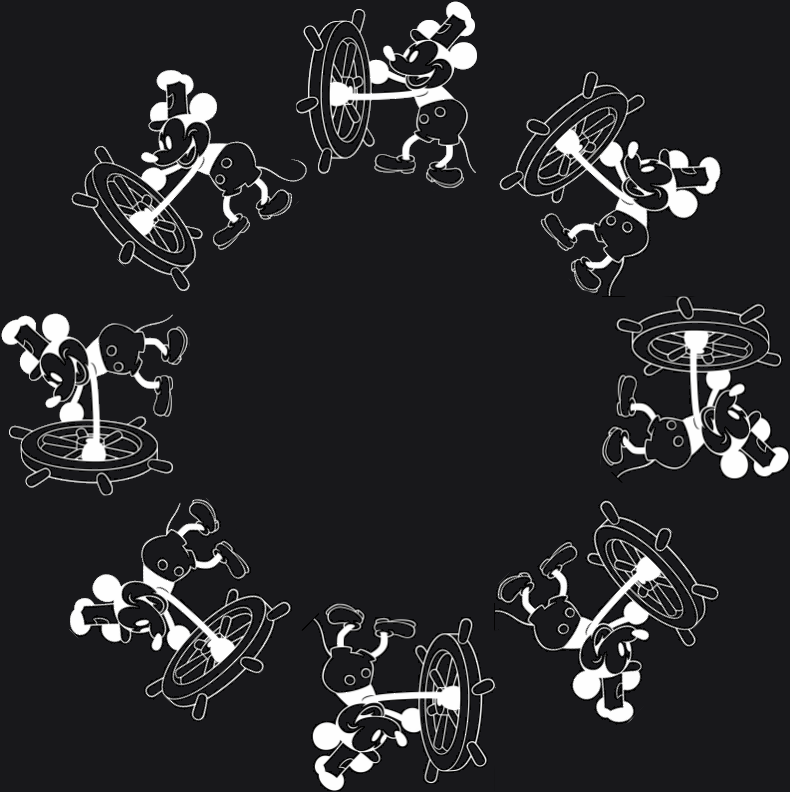
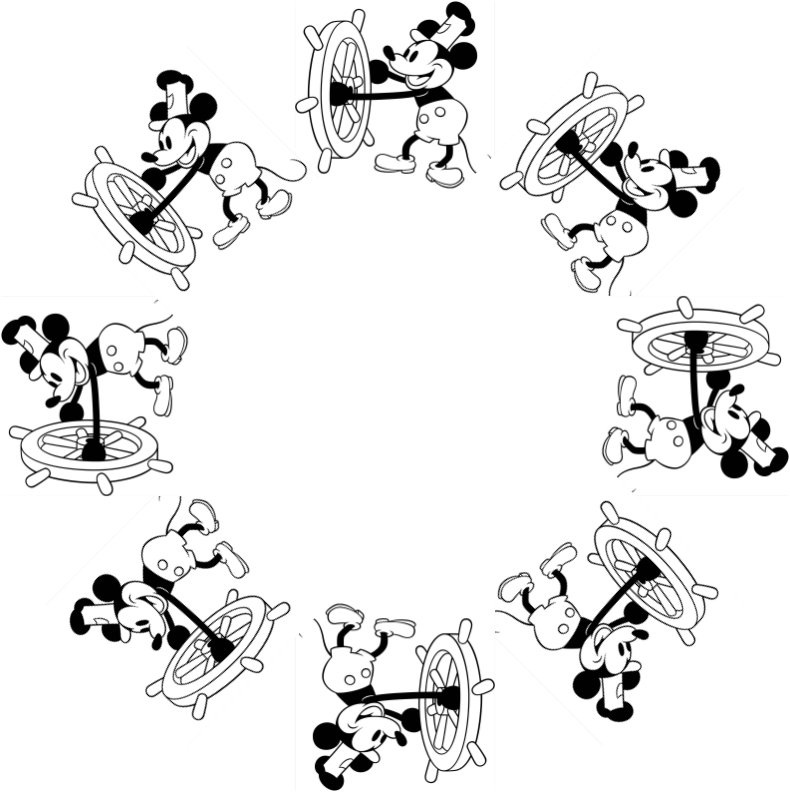
dilation symmetry

A more unusual symmetry is an image with dilation symmetry. You can zoom in, or out, and at some point, the image looks the same again. Here we have created Willie with dilation symmetry. If you magnify the image 2x, it looks the same.

circles packed on circles

Another example of dilation symmetry uses a circle packing. A ring of circles, each tangent to its neighbor, forms the basic unit. That ring of circles is then scaled and rotated to be tangent to another ring. The image is determined by a single parameter, the number of circles in each ring:

Indeed, if you change the color of a circle in each ring, and do the same to its clockwise neighbor in the next smaller ring, you get a logarithmic spiral. Remarkably, although our eye cannot discern it, the spiral circles the center infinitely many times!

circles packed on a spiral

Circles packed on circles have dilation symmetry, but also rotational symmetry and reflective symmetry. Can we pack circles in a way that has only dilation symmetry?

One way to do this is by putting the circles with their centers on a logarithmic spiral. And to be packed, we want each circle tangent to the next in the spiral, as well as to the nearest circles in the previous and next arms of the spiral.