Lexen's Tricurve

We were introduced to tricurves by their inventor, Tim Lexen. To make a tricurve, you begin with half of a circle, divided into three arcs in the ratio 1:2:3…

Those three arcs can then be joined at their ends to form the tricurve shape:

Remarkably, the interior angles of the tricurve have the same proportions as the edge lengths! This is part of the reason the tricurve works so well for creative tiling.

Notice that because the shorter edges have the same total length as the longest edge, you can cover a long edge with the two shorter edges.

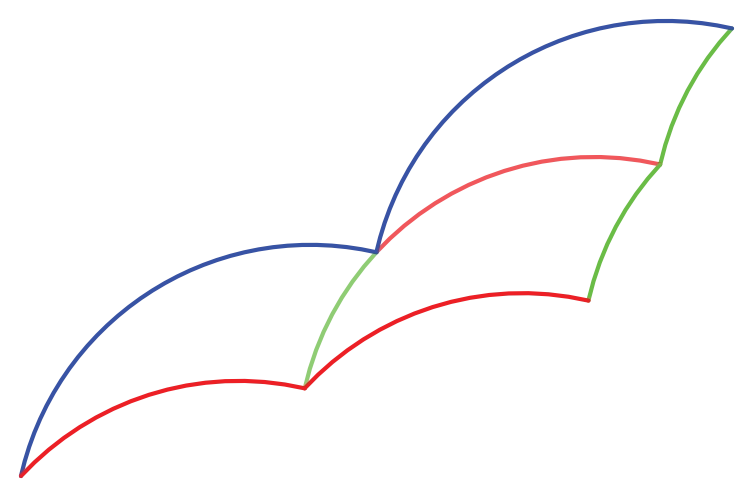
This demonstrates visually how our tricurve, with its curved edges, doesn't satisfy the triangle inequality.